Building on the thoughts expressed in Optics for Wildlife Photography and Field of View and Reach, I made a graph to compare field of view, effective aperture, and pixel count for various wildlife-oriented camera systems.
But first, let's simply compare aperture diameters. iPhone 15 Pro Max's longest lens has a physical focal length of 15.7mm and an f-number of 2.8, giving it an aperture diameter of 15.7mm/2.8 = 5.6mm. The point-and-shoot Sony HX99 has a max physical focal length of 118mm and an f-number of 6.4 at that focal length, giving it an aperture diameter of 18mm. That's 3.4 more stops than the iPhone (because log(18**2)/log(2) - log(5.6**2)/log(2) = 3.4). Let's compare more:
I grouped these lenses into tiers based on their aperture diameter, but I named the tiers after their typical physical sizes: "Small", "hiking", "big", and "really big". A few primes manage to punch above their physical sizes: The Nikon F-mount 300mm F4 is a small lens with "hiking"-tier brightness, and a few hiking-friendly primes (400mm 4.5, 500mm 5.6, and 600mm 6.3) have "big lens"-tier brightness.
Lenses are frequently dimmer (and shorter) than their nominal specs suggest, amounting to perhaps 1/6th stop of aperture diameter. That effect isn't reflected above. As far as I can tell, it doesn't matter much, since most lenses "cheat" by about the same amount, at least if they are from Japanese/CIPA-member companies.
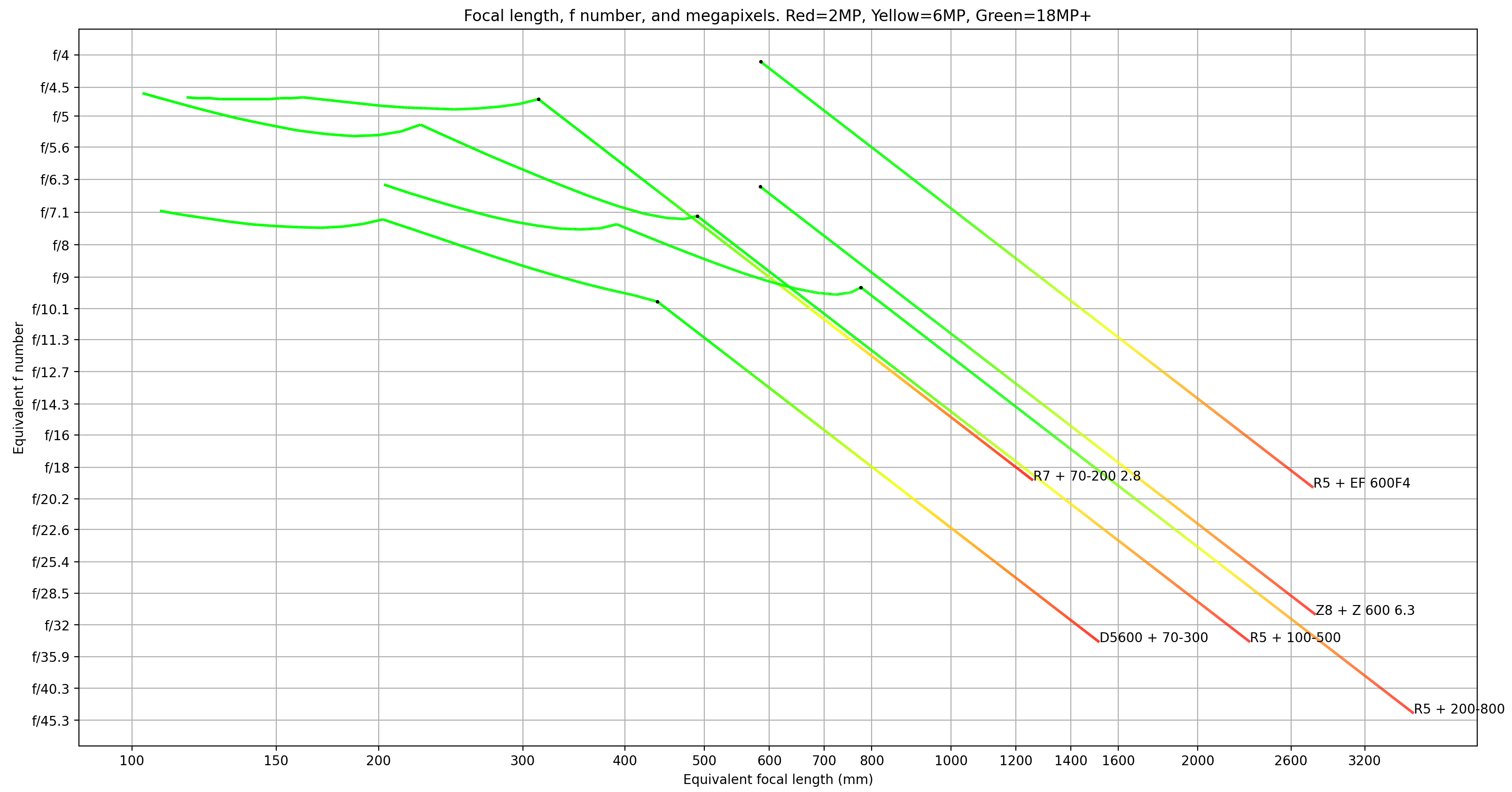
Aperture diameter is important, but just knowing that number at a lens' max focal length doesn't tell the whole story, especially for zoom lenses. The "whole story" has many more dimensions, but let's consider just two more: field of view and pixel count. For familiarity, I will plot equivalent f-number instead of aperture diameter:
This shows six camera systems across four tiers. Details:
To conclude, here's a picture taken with the "small"-tier 70-300 6.3 lens, cropped to an equivalent focal length of 994mm. ISO 560, 1/1000 sec. You can find the equivalent f-number on the graph above.