Many considerations matter, but I will disregard most of them as I try to get at the core optical dimensions that matter for a wildlife photography camera system. I'll disregard the brightness of the scene, the subject's size and reflectivity, and its willingness to hold still. I'll disregard vibration reduction, weight, weather resistance, handling, field of view, minimum focus distance, and the likelihood that shutter noise scares the subject. I'll disregard autofocus performance, frames-per-second, pre-release shooting, rolling shutter, buffer depth, and dynamic range. And I'll disregard bokeh, distortion, and lens flaring.
I'll consider two scenarios. In the first scenario, I can't get as close as I'd like; this usually means that the subject doesn't fill the frame (although the desired framing depends on what I'm going for). I'll have to crop afterwards, perhaps heavily. In this scenario, the distance to the subject is fixed for all camera systems. In the second scenario, I can get as close as I'd like (or wait for the subject to approach as close as I'd like). I'll "zoom with my feet" and fill the frame with any camera system, and do hardly any cropping afterwards. In both scenarios, I want
But relevant system characteristics depend on the scenario.
In the first scenario, the number of subject photons that reach the sensor is primarily determined by the diameter of the aperture (a.k.a. "objective lens size"). Transmittance of the lens + filter also matters, but this quantity does not vary drastically (?), so I haven't bolded it. And the atmosphere matters, although it will have the same effect for all camera systems at a fixed distance. The recently-released Canon RF 200-800mm f/6.3-9 has a maximum aperture diameter of 800mm/9 = 88.9mm at the long end. (At 637mm, its brightest f-number is f/8, so its max aperture diameter is 637mm/8 = 79.6mm at that focal length.) By comparison, the Nikon 180-600mm f/5.6-6.3 has a max aperture diameter of 600mm/6.3 = 95.2mm. So the Nikon's max diameter is 7% larger (because 95.2/88.9 = 1.07). That's 1/5th of a stop (because log(1.07)/log(sqrt(2)) = 0.195 = 1/5th). Note that attaching a teleconverter doesn't affect aperture diameter.
The number of pixels on the subject will be determined by focal length (which determines the size of the subject's projected image on the sensor) and pixel density. But it would be a bit premature to conclude by simply combining those two numbers into a single dimension ("pixels on subject"), unless the lens is perfectly sharp (which is impossible) and the sensor has negligible read noise.
In reality, lenses are not perfectly sharp. Therefore, a longer focal length decreases the effect of lens imperfections by projecting a subject's photons into a larger image. Let's illustrate with an informal thought experiment: Consider two lenses with identical (but imperfect) sharpness and different focal lengths. The "long" lens has twice the focal length of the "short" lens. If you attach them to the same camera body and point them at MFT targets, and the MTF target distance is proportional to the focal length, then you get the same images, which look something like this:
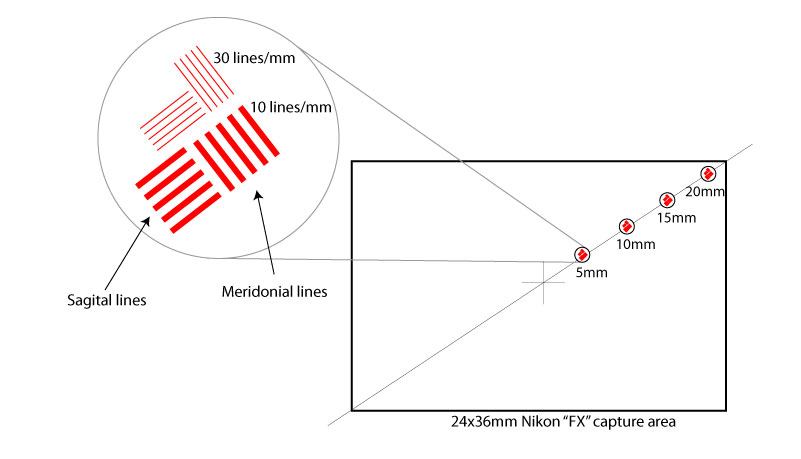
MTF target. © Nikon.
(Okay, maybe the images aren't perfectly identical, but they correspond to identical MTF charts, which is why we say the lenses have the same sharpness. Pretend the images are identical.) Suppose the images have a line the thickness of two pixels, with a "smudge" the thickness of another two pixels. Now take the body off the long lens, and swap it for a body with 1/4th the pixel count. The same line on the long system now has the thickness of one (larger) pixel, and a corresponding "smudge" of about one pixel. When we pan away from the MTF targets and focus on a bird a fixed distance away, the bird's feathers happen to look just like another MTF target on the short system, but they are now magnified to 2x height on the longer system. A line/feather on the longer system is magnified to two-pixel thickness (since the bird is half the distance as the longer system's MTF target), but the smudge is still approximately just one pixel, if we boldly assume the smudge is a property of the lens independent of the target distance. On the shorter system, the same feather still has two pixels of thickness and two pixels of smudge. In summary, the fixed-distance subject appears sharper on the longer system, despite both systems having the same number of pixels on the subject and using equally sharp lenses.
Therefore, even if your sensor had infinite resolution, you wouldn't just want your sharpest lens for photographing a fixed-distance stationary subject from a tripod. You'd want the lens that is sharpest after adjusting for focal length. You'd adjust for focal length by cropping or attaching a teleconverter; let's consider the latter because there is relevant MTF data available. Attaching a teleconverter to adjust focal length will degrade the system's MTF chart, even if it's a "perfect" teleconverter. For example, the Canon RF 100-500mm F4.5-7.1 is sharper than the RF 800mm, but after attaching a hypothetical, "perfect" 1.6x teleconverter to the first lens to adjust for focal length, the sharpness would be about even. (Reference MTF charts with real teleconverters: 800mm, 500mm + 1.4x, 500mm + 2x. I think it's safe to assume that most of the degradation is due to adjusted focal length, not due to imperfections in the teleconverters.) I wish I knew a formula to predict the effect of "adjusting focal length with a perfect teleconverter" on the MTF, but I'm not aware of one. I made a dpreview.com forum post on this topic.
Moving on to the last characteristic that matters in this scenario: A sensor's pixel density is derivable from its pixel count and dimensions. Since doubling focal length will double a projected image's height (and quadruple its area), therefore, it's easier to keep "pixels on subject" in mind if I calculate pixels per sensor length rather than pixels per sensor area. I'll measure length in inches because a full-frame sensor's height is almost an inch (24 mm = 0.94 inch).
Of course, the marginal benefit of additional pixels on the subject decreases with shot noise, read noise, and imperfectly sharp lenses.
In the second scenario, I can "zoom with my feet" and frame the subject perfectly. In this scenario, the number of subject photons that reach the sensor is primarily determined by the equivalent f-number, which is f-number multiplied by crop factor. (If the perfect framing is 4:3, then the Micro Four Thirds crop factor is 1.85x, and if the perfect framing is 3:2, then the Micro Four Thirds crop factor is 2.08x.) Transmittance of the lens + filter also matters, as does the atmosphere. In this scenario, systems with a shorter equivalent focal length have less atmosphere in the way.
The number of pixels on the subject, given "perfect" framing, is just proportional to the pixel count of the sensor. Of course, the same caveats about lens sharpness and read noise apply. It's also worth noting that, if I don't crop, all modern sensors have a lot of pixels, so more is only better if the viewer will want to zoom in on the subject's face, or if I use a large-format printer.
In summary:
When I can't get as close as I'd like to the subject, the important system characteristics are:
Sensor read noise also matters, but is usually minor.
When I can get as close as I'd like to the subject, the most important system characteristic is equivalent f-number. Additional "light related" factors are equivalent focal length (shorter is better if the air isn't clear) and transmittance. "Pixel related" factors are the sensor's pixel count, lens sharpness, and read noise.
It isn't easy to get close enough to small, shy birds. If you can invest the time and effort to get into position and fill the frame, then you're in scenario #2, and you'll want to bring a fast lens. Since I'm interested in birding and hiking as well as amateur wildlife photography, I'm usually in scenario #1. And Canon's apparent strategy of making longer, slower consumer lenses makes a lot of sense to me.
Some smartphones have "telephoto" camera modules that actually have smaller aperture diameters than the main camera module, which means that the best choice for dark, distant subjects may actually be the main camera (perhaps with 2x digital zoom to avoid pixel binning), not the telephoto. On the Samsung S22, this effect is present but negligible (3% smaller aperture diameter). On the iPhone 14 Pro Max, the telephoto's diameter is 18% narrower than the main, although the effect is reversed with the iPhone 15 Pro Max's "periscope" lense (41% larger diameter than main).
The S22's equivalent f-number is f/7.2 while the Pixel 7's equivalent f-number is f/6. Since the Pixel 7's aperture diameter is also about 20% larger than the S22's, it's fair to say that the Pixel 7 is half a stop brighter in all scenarios (excluding the ultra-wide modules). Spreadsheet for reference. More details in my post about smartphone camera specs.
Updated 2024-03-10.

This work is licensed under a Creative Commons Attribution 4.0 International License.